


As an example, in Figure 1 above, if the cue ball was rolling forward and had a hard right spin, the cue ball would come off the rail at an angle much more oblique (more parallel to the rail) than expected. This motion can be present in two forms: (1) Forward/Backward rotation, and (2) Side Spin (commonly referred to as Spin or English). Cue ball rotational at the time of impact has a MASSIVE affect on rebound angle. For cue balls hit really soft, the angle will be fatter (more oblique).ģ. If you hit the cue ball hard, the angle of rebound will be sharper (more acute). Conversely, for shots into the rail that are nearly perpendicular, the rebound will be even more perpendicular (more acute) than theory suggests.Ģ.
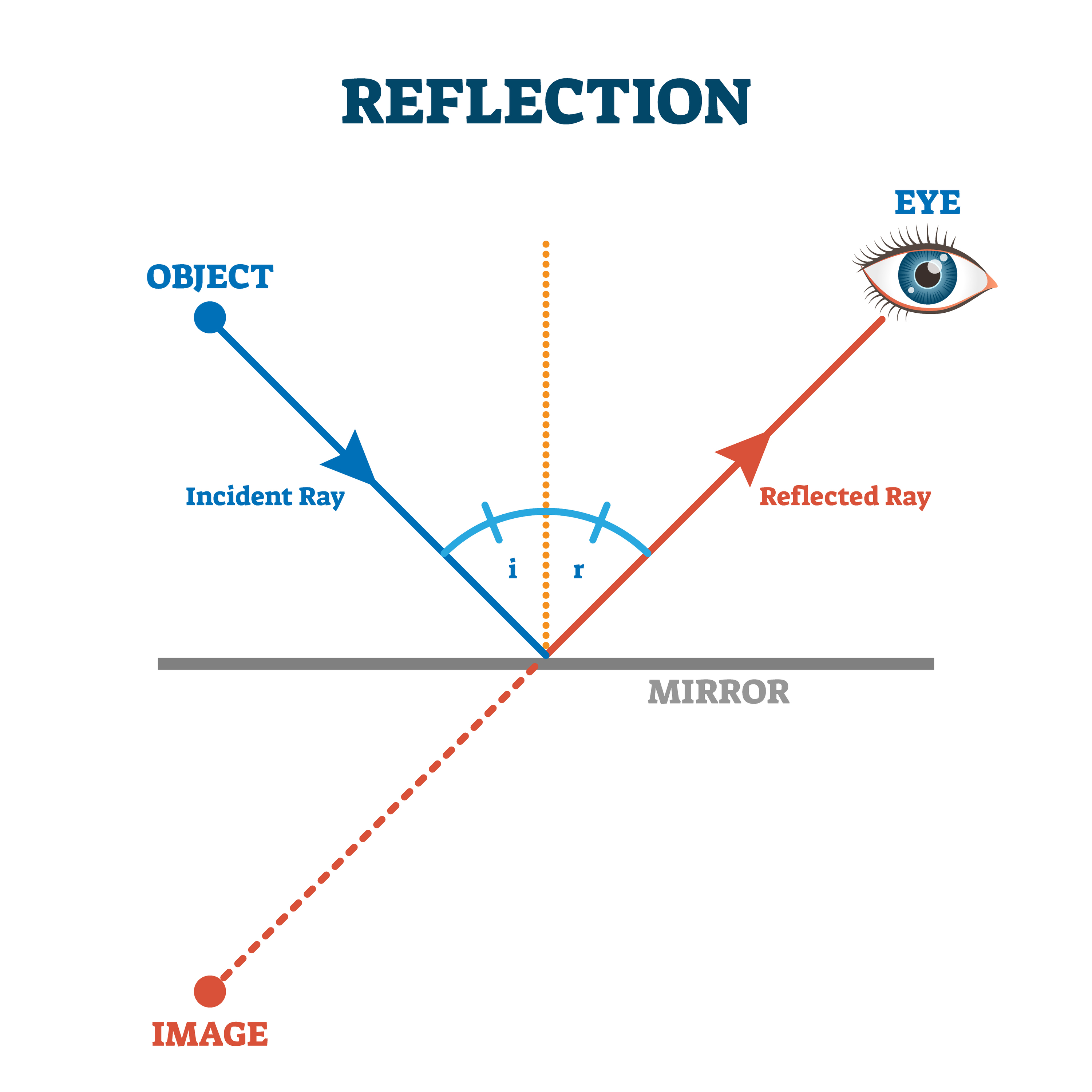
For very large angles of incidence (the cue ball is approaching the rail at a shallow angle), the angle of rebound will be even shallower than the theoretical value (more oblique). Here are the general rules for determining the influence of these factors:ġ. How much will it be modified? Unfortunately, you have to go to the table and experiment with these factors to get a feel for how much they influence the rebound angle. However, if you vary any of these three factors, the angle of reflection will be modified from the theoretical value. Under these three conditions, the angle of reflection will almost exactly equal the angle of incidence. This is actually a very accurate guideline for predicting the path of a cue ball bouncing off a rail under the following three conditions: (1) if the cue ball is rolling naturally (not over spinning, sliding, or rotating backwards), (2) if the cue ball has a very slight horizontal rotation to it (in this case, a slight right spin, also known as “Running English”), and (3) if the cue ball is hit with normal speed (between 3 and 7 on the Arm Calibration scale from my Novempost). In figure 1, I show the classic concept from physics, where the angle of incidence equals the angle of reflection. Although this approach is very accurate when applied to light waves or other forms of electromagnetic radiation (with little or no mass), this rule of thumb can be highly influenced by other forces when applied to a real world setting that is filled with rolling and spinning spheres of significant mass. The generally accepted rule of thumb for predicting the angle of rebound goes something like this: “The angle of incidence equals the angle of reflection.” This is a concept borrowed from classical physics. When a cue ball rolls toward a cushion, hits the cushion and rebounds back, how do we predict the angle the cue ball will take when it leaves the cushion? That seems like an easy thing to predict, huh? Well, in some ways it is.

I’ll start with the Angle of Reflection, then later today when hopefully I feel a little better, I’ll write about the next topic, Speed after Collision. The vertical distances from \(A\) and \(B\) to the mirror are \(a\) and \(b\) respectively.Hello World! Sorry for the tardy post, I’ve been in bed for two days sick, but hey baby, I’m back! Since I’m a day behind, I’ll do two posts today. The horizontal distance between \(B\) and the normal is therefore \(d-x\). In the diagram below we have written \(d\) for the horizontal distance between \(A\) and \(B\) and \(x\) for the horizontal distance between \(A\) and the normal. We can derive the law of reflection from Fermat’s principle mathematically, using a little calculus. For another method of approaching this optimisation problem, see Calculus of variations. It’s an example of a principle of least action: the assumption that, when faced with a choice, nature always chooses the option that involves the least effort. This idea is known as Fermat’s principle, after the 17th century mathematician Pierre de Fermat (although others had come up with the principle before him). Since light travels at constant speed (it doesn’t speed up or slow down), assuming that it travels along the path of shortest distance (via the mirror) is equivalent to assuming it travels along the path that takes the shortest time.


 0 kommentar(er)
0 kommentar(er)
